How To Set Up Proportions
Proportions: Simple Exercises
Solving proportions is simply a matter of stating the ratios equally fractions, setting the 2 fractions equal to each other, cross-multiplying, and solving the resulting equation. The practice prepare will probably commencement out by request for the solutions to straightforward simple proportions, merely they might use the "odds" notation, something like this:
-
Observe the unknown value in the proportion: 2 :x = iii : ix.
Okay; they've given me to ratios, in "odds" notation, and set up them equal. This creates a proportion:
Content Continues Below
ii : x = three : 9
My commencement step volition be to convert the colon-based odds-note ratios to fractional class, so I get an equation with 2 fractions:
Then I'll solve the proportion. I could cross-multiply, and and then divide back off, but I think I'll use the informal shortcut, like was illustrated earlier:
![]()
Using this method, I always multiply across in the management that has regular numbers on either end. In this example, I'll multiply the ii and the 9 (going from the tiptop-left to the lesser-right), and then I'll divide past the iii (going from the meridian-right effectually to the bottom-left, where the variable is):
![]()
If I have to "show my piece of work", I'll include my fractional equation with the arrows. My reply is:
x = half dozen
-
Detect the unknown value in the proportion: (2x + 1) : ii = (x + ii) : 5
Okay; this proportion has more variables than I've seen previously, and they're in expressions, rather than standing by themselves. So this is gonna be a cross-multiplying solution.
Start, I catechumen the colon-based odds-notation ratios to fractional course:
Then I solve the proportion, starting by cross-multiplying:
5(2x + one) = 2(x + 2)
1010 + 5 = iix + 4
viiix = −one
I wasn't expecting a fraction, simply it's a perfectly valid answer (which I tin check, if I want, by plugging it dorsum into the original equation).
Once you've solved a few proportions, you lot'll likely then move into word problems where you'll first accept to invent the proportion, extracting it from the word problem, before solving information technology.
-
If twelve inches correspond to xxx.48 centimeters, how many centimeters are there in thirty inches?
I volition fix up my ratios with "inches" on acme (merely because; there's no logic or particular reason for information technology), and will use the alphabetic character " c " to stand for the number of centimeters for which they've asked me. So here's my gear up-up:
One time I have my proportion, I can solve. In this case, I can use the shortcut method:
![]()
c = 76.2
Looking back at how I defined the variable, I see that c stands for "the number of centimeters". The question asked for "how many centimeters?", not "what value?", so I demand the unit of measurement "centimeters" on my answer.
76.2 cm
I could have used whatever alphabetic character I liked for my variable. I chose to use " c " because this helped me to retrieve what the variable was representing; namely, "centimeters". An x would only tell me that I'm looking for "some unknown value"; a c can remind me that I'yard looking for " c entimeters".
Don't autumn into the trap of thinking that you take to use x for everything. You tin use whatever variable y'all find almost helpful.
-
A metal bar 10 feet long weighs 128 pounds. What is the weight of a similar bar that is two feet iv inches long?
First, I'll need to convert the "two feet four inches" into a anxiety-only measurement. Since one foot contains twelve inches, then iv inches is 4-twelfths, or one-3rd, of a pes. So the length, converted to feet only, is:
I will gear up my ratios with the length values on top (because I happened to pick that ordering, probably because the length info came before the weight info in the exercise). I'll employ this set-up to make sure that I write out my proportion correctly, and and so I'll solve for the required weight value. By the fashion, since I'k looking for a weight, I'm going to utilize west as my variable.
I can use the shortcut method for solving this proportion, so I'll multiply crossways in the i direction, and and then hook back and divide going in the other direction:
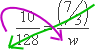
Since this is a "real world" give-and-take trouble, I should probably circular or decimalize my exact fractional solution to get a applied "real world" sort of number. To be on the safe side, though, I'll give both the "exact" (partial) form and also the rounded (more real-world) form:
The bar volition weigh , or about 29.87, pounds.
-
The tax on a property with an assessed value of $70,000 is $one,100. What is the assessed value of a property in the same commune, if the tax on that property is $one,400?
The logical footing for answering this question is the unstated assumption that all backdrop in the same district are assessed at the aforementioned percentage rate.
If this question were being asked in the homework for the section on "percent of" discussion bug, then I would have the tax rate as a percent from the info they gave me for the first property; and then I would accept dorsum-solved, using the rate I'd just found, for the value of the second property. All the same, since this question is being asked in the section on proportions, I'll solve using a proportion.
They've given me two categories of things: assessed values of properties, and the amounts of taxes paid. My ratios will then use these two categories. I will set upwardly my ratios with the assessed valuation on top (considering that's what I read first in the exercise), and I volition use " v " to represent the value that I need to notice.
I'll use the shortcut method for solving, multiplying the 70,000 and the 1,400 in 1 direction, and and then dividing by the i,100 going in the other management:
![]()
Since the solution is a dollars-and-cents value, I must round the final answer to ii decimal places; the "verbal" grade (whether repeating decimal or fraction) wouldn't brand sense in this context. Then my respond is:
The assessed value is $89,090.91.
-
One piece of pipage 21 meters long is to exist cut into ii pieces, with the lengths of the pieces being in a ii : five ratio. What are the lengths of the pieces?
I'll label the length of the short piece as " s ". Then the long piece, being what was left of the original piece subsequently I cut off s meters, must accept a length of 21 −south . And so my ratio, in fractional (rather than in odds) format, is:
Because there are two parts of this proportion that contain variables, I can't utilise the shortcut to solve. Instead, I'll cross-multiply, and proceed from there.
2(21 − s) = 5south
42 − 2s = fivedue south
42 = 7s
6 = s
Referring dorsum to my set up-upwards for my equation, I come across that I defined " due south " to correspond the length of the south horter piece, with the unit of measurement of length being meters. Then the length of the longer slice is given by:
21 − southward = 21 − 6 = fifteen
Now that I've constitute both required values, I can give my answer, complete with the right units:
six meters and 15 meters
In the last practise above, if I had not defined what I was using " s " to correspond, I could easily accept overlooked the fact that " due south = vi" was not the reply the practise was wanting. Try always to conspicuously define and label your variables. Also, be sure to get dorsum and re-check the word problem for what information technology actually wants. This exercise did non enquire me to discover "the value of a variable" or "the length of the shorter slice". By re-checking the original exercise, I was able to provide an appropriate response, being the lengths of each of the two pieces, including the correct units of meters.
Source: https://www.purplemath.com/modules/ratio4.htm

0 Response to "How To Set Up Proportions"
Post a Comment